Separation Logic

对可变共享数据结构的研究导向了在逻辑层面的若干独立发现，在2002年由J.C. Reynolds正式在LICS’02上提出分离逻辑的概念。分离逻辑既指一种谓词逻辑的扩展，也指以此种逻辑进行断言的Hoare Logic扩展及其推理系统。

Motivation

对于堆上的数据结构，如果仅使用谓词逻辑进行描述会非常复杂，也难以scale。究其原因，通常对这类程序进行分析时，往往需要对数据结构间的共享/别名情况进行限制，譬如：

$$\begin{gathered} (\exists \alpha ,\beta .\text{list}\alpha i\wedge \text{list}\beta j\wedge {\alpha }_0^{†}={\alpha }^{†}\cdot \beta ) \\ \wedge (\forall k.\text{reach}(i,k)\wedge \text{reach}(j,k)\Rightarrow k=\text{nil}), \end{gathered}$$

其中的reach是归纳定义的谓词。公式的后一部分表示i和j代表的链表不相交。

除了所关心的结构本身是否共享内存，一个严谨的证明还需要对程序没有涉及到的堆的其他位置的情况进行刻画。比如，通常这些内存地址应该不变：

$$\begin{array}{rl}& (\exists \alpha ,\beta .\text{list}\alpha i\wedge \text{list}\beta j\wedge {\alpha }_0^{†}={\alpha }^{†}\cdot \beta )\wedge \text{list}\gamma x\\ & \wedge (\forall k.\text{reach}(i,k)\wedge \text{reach}(j,k)\Rightarrow k=\text{nil})\\ & \wedge (\forall k.\text{reach}(x,k)\wedge (\text{reach}(i,k)\vee \text{reach}(j,k))\Rightarrow k=\text{nil}).\end{array}$$

分离逻辑可以解决上述问题，关键点在于这些情况均可用堆的「分离」刻画，且分离逻辑公式可以从堆的局部属性出发。

Assertion Language

Syntax

在FOL的基础上增加：

Syntax	Intention
emp	empty heap
$e\mapsto e$	singleton heap
$p\ast p$	separating conjunction	分离与
$p⊸p$	separating implication	分离蕴涵

Semantics

对堆的建模有多种方式，比如可以假设堆地址和变量值不在一个domain。这里假设堆的地址都是整数（好处是可以支持指针算术运算），即

• Addresses $\subseteq$ Integers $\subseteq$ Values
• Heaps = ${\bigcup }_{A\subseteq Addresses}^{\text{fin}}(A\to \text{Values})$

此时程序的状态由标准的store s以及堆h组成。可以类似地在其上定义程序的小步操作语义，不过需要注意的是，对内存的load和store都需要先在s上求地址的值，如果这个值不是一个地址（不属于Addresses），程序abort。

上述语义的一个重要性质在于对堆进行限制后的执行。如果被排除的地址被解引用或释放，则程序abort，否则限制下的执行不更改被排除部分的堆：

• If $⟨c,(s,h)⟩{⇝}^{\ast }\mathbf{abort}$, then $⟨c,(s,h_0)⟩{⇝}^{\ast }\mathbf{abort}$.
• If $⟨c,(s,h)⟩{⇝}^{\ast }(s^{\prime },h^{\prime })$ then $⟨c,(s,h_0)⟩{⇝}^{\ast }\mathbf{abort}$ or $⟨c,(s,h_0)⟩{⇝}^{\ast }(s^{\prime },h_0^{\prime })$, where $h_0^{\prime }\perp h_1$ and $h^{\prime }=h_0^{\prime }\cdot h_1$.
• If $⟨c,(s,h)⟩\uparrow$ then either $⟨c,(s,h_0)⟩{⇝}^{\ast }\mathbf{abort}$ or $⟨c,(s,h_0)⟩\uparrow$.

分离与

$[p_0\ast p_1{]}_{\text{asrt}}sh\text{ iff }\exists h_0,h_1.h_0\perp h_1\text{ and }{h}_0\cdot h_1=h\text{ and }[p_0{]}_{\text{asrt}}s{h}_0\text{ and }[p_1{]}_{\text{asrt}}s{h}_1,$

分离与和逻辑与的区别：

1. $x\mapsto 3,y\ast y\mapsto 3,x$:
2. $x\mapsto 3,y\wedge y\mapsto 3,x$:

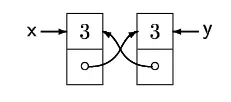
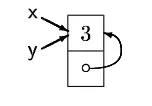
这种差异来源于$e\mapsto e$刻画的并不是全局的性质，而是局部性质：其模型h必须是只包含一个特定地址(s e)。如果对堆的其它位置没有约束，可以写作$e\mapsto e\ast true$，或者用语法糖写作$e\hookrightarrow e$

分离蕴涵

$[p_0\to \ast p_1{]}_{\text{asrt}}sh\text{ iff }\forall h^{\prime }.(h^{\prime }\perp h\text{ and }[p_0{]}_{\text{asrt}}s{h}^{\prime })\text{ implies }[p_1{]}_{\text{asrt}}s(h\cdot h^{\prime }).$

常见性质

分离逻辑是一种Substructural Logic.

1. 分离与有结合律、交换律
2. emp是分离与的单位元
3. 分离与对析取有分配律，对合取只有一侧成立$(p_1\wedge p_2)\ast q\to (p_1\ast q)\wedge (p_2\ast q)$

满足特定情况下具有更好的性质：

• pure assertion: 不包含emp和$\mapsto$，此时分离与、分离蕴涵和相应的逻辑连接词等价
• intuitionistic assertion: 如果h满足，则h的扩展h’也满足
• strictly exact assertion: 公式在给定s下只被一个h满足

Specification Language

使用分离逻辑作为断言语言的Hoare Logic，此时三元组额外要求程序执行中不会abort

此时，霍尔逻辑中的Constancy规则（在结论的前后置条件都逻辑与上一个公式）不再可靠，取而代之的是重要的Frame规则：

$\frac{\{p\}c\{q\}}{\{p\ast r\}c\{q\ast r\}}$

where no variable occurring free in r is modified by c .

Frame规则的重要性在于允许使用局部的规约：

To understand how a program works, it should be possible for reasoning and specification to be confined to the cells that the program actually accesses¹. The value of any other cell will automatically remain unchanged

Related

• 数理逻辑

Footnotes

1. memory footprint ↩