CAV20, Local Reasoning About the Presence of Bugs: Incorrectness Separation Logic
Motivation
Using SL, symbolic execution need not begin from a “main” program, but rather can “begin anywhere” in a codebase, with constraints on the environment synthesized along the way.
this paper take a step towards transferring the local reasoning techniques from the world of program verification to that of bug catching.
Challenge: the original SL model, based on partial heaps, is incompatible with local, under-approximate reasoning.
For instance, from this following triple
if we apply Frame rule:
The presumption here is false, so the under-approximate triple is invalid. However, this does not cause problem in classical Hoare logic.
Extra Syntax
Compared to original SL, ISL introduces an explicit symbol for freed memory.
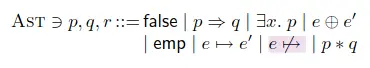
Proof System
Note that in Separation Logic, we only need to specify local specification needed for the statement. Thus the rule for assignments, skip etc. are different.


Incorrectness Logic 的 Separation Logic 扩展。三元组使用与错误逻辑相同的解释(后向可达、下近似)。核心是为了让 Frame 规则仍然成立,需要在断言语言中显式引入刻画内存已释放的语法(SL 原本是不区分 emp和已释放的堆)
We observe that the original SL model, based on partial heaps, is incompatible with local, under-approximate reasoning. The problem is that the original model does not distinguish a pointer known to be dangling from one about which we have no knowledge; this in turn contradicts the frame rule for under-approximate reasoning.
注意 Fig5 中的一些推导规则相比SL 以及经典霍尔逻辑有所修改,主要是为了契合下近似,前置条件尽量强(便于弱化),后置条件尽量弱(便于加强)。
实现在 Infer 的分析工具 Pulse 中,其底层是基于Bi-abduction 的自动推理/符号执行(自然,因为 CONS 规则方向相反,bi-abduction 的方向也相反)。这使得每一步只需要关注当前语句的 spec,然后综合出 frame/antiframe 即可。同时 frame 可以直接由 frame 规则分离与到前置条件上。
Annotations
“Using SL, symbolic execution need not begin from a “main” program, but rather can “begin anywhere” in a codebase, with constraints on the environment synthesized along the way.” (Raad et al., 2020, p. 226)
“we take a step towards transferring the local reasoning techniques from the world of program verification to that of bug catching.” (Raad et al., 2020, p. 226)
“We observe that the original SL model, based on partial heaps, is incompatible with local, under-approximate reasoning. The problem is that the original model does not distinguish a pointer known to be dangling from one about which we have no knowledge; this in turn contradicts the frame rule for under-approximate reasoning.” (Raad et al., 2020, p. 226)
“However, we recover the frame rule for a refined model with negative heap assertions of the form x → , read “invalidated x”, stating that the location at x has been deallocated (and not re-allocated).” (Raad et al., 2020, p. 226)
“refers to memory that has been invalidated. As we describe shortly, this information is tracked in Pulse with an invalidated heap assertion.” (Raad et al., 2020, p. 228)
“The ability to go below the strongest post soundly is a hallmark of under-approximate reasoning: it allows for compromise in an analyzer, where we might choose, e.g., to limit the number of paths explored for efficiency reasons, or to concretize an assertion partially when symbolic reasoning becomes difficult” (Raad et al., 2020, p. 229)
“by composing the standard semantics of SL [41] and the semantics of incorrectness logic [35]. Interestingly, this simplistic approach does not work.” (Raad et al., 2020, p. 230)
“In over-approximate reasoning this does not cause a problem since an inconsistent precondition renders an over-approximate triple vacuously valid. By contrast, an inconsistent presumption does not validate under-approximate reasoning” (Raad et al., 2020, p. 230)
“consider a modified model in which the knowledge that a location was previously freed is a resource-oriented fact, using negative heap assertions. The negative heap assertion x → conveys more knowledge than the loc(x) assertion. Specifically, x → conveys: 1) the knowledge that x is an addressable location; 2) the knowledge that x has been deallocated; and 3) the ownership of location x.” (Raad et al., 2020, p. 230)
(Raad et al., 2020, p. 231) 这里是用frame规则应用pb-ok,再分离与上x=a
“x := malloc() x := alloc() + x := null” (Raad et al., 2020, p. 232)
“assertions describe sets of states, where each state comprises a (variable) store and a heap” (Raad et al., 2020, p. 233)
“ISL triples are local in that the states described by their presumptions only contain the resources needed by the program. For instance, as skip requires no resource for successful execution, the presumption of Skip is simply given by emp, which remains unchanged in the result.” (Raad et al., 2020, p. 233)
“In general, in over-approximate logics (e.g., SL) the aim is to weaken the preconditions and strengthen the postconditions of specifications as much as possible. This is to ensure that we can optimally apply the Cons rule to adapt the specifications to broader contexts. Conversely, in under-approximate logics (e.g., ISL) we should strengthen the presumptions and weaken the results as much as possible, since the implication directions in the premise of Cons are flipped.” (Raad et al., 2020, p. 236)
(Raad et al., 2020, p. 237) alloc1/alloc2
“We use the designated value ⊥ ∈ Val to track those locations that have been deallocated.” (Raad et al., 2020, p. 237)
“Note that for all C, and (σp, σq) ∈ C , the (domain of the) underlying heap in σp monotonically grows from σp to σq and never shrinks.” (Raad et al., 2020, p. 238)
“This is in contrast to the original SL model [28], where deallocation removes the given location from the heap, and thus the underlying heap may grow or shrink” (Raad et al., 2020, p. 238)
“the ISL proof rules are sound : if a triple [p] C [ : q] is derivable using the rules in Fig. 5, then |= [p] C [ : q] holds.” (Raad et al., 2020, p. 238)
“ISL lends itself naturally to the definition of forward symbolic execution analyses.” (Raad et al., 2020, p. 241)
“allows us to infer valid ISL triples automatically for a given piece of code, with the goal of finding only true bugs reachable from an initial state.” (Raad et al., 2020, p. 241)
“Ideally, one would find specifications for all procedures in the codebase, all the way to an entry-point (e.g., the main() function), thus proving the program safe. In practice, however, virtually all sizable codebases have bugs, and known abstract domains are imprecise when proving memory safety for large codebases” (Raad et al., 2020, p. 241)
“Pulse approaches bug reporting more directly: by looking for them. It infers under-approximate specifications, while recording invalidated addresses. If such an address is later accessed, a bug is reported soundly, in line with the theory.” (Raad et al., 2020, p. 242)
“As is standard in SL-based tools [4,11], our abstract states consist of ∗-conjoined predicates, with the notable addition of the invalidated assertion and omission of inductive predicates. The latter are not needed because we never perform the over-approximation steps that would introduce them.” (Raad et al., 2020, p. 242)
“To ensure termination, loops are unrolled up to a fixed bound Nloops, borrowing from symbolic bounded model checking [12]. These two ideas avoid the arduous task of inventing join and widen operators” (Raad et al., 2020, p. 242)
“The unknowns M and F in the bi-abduction question p ∗ F q0 ∗ M have analogous counterparts in over-approximate bi-abduction; but, as in the Cons rule, their roles have flipped: the frame F is abduced, while the missing M is framed (or anti-abduced ).” (Raad et al., 2020, p. 243)
“Pulse does not use Alloc2, and thus prunes further paths.” (Raad et al., 2020, p. 245)
“There is a fundamental tension in correctness-based techniques, most thoroughly explored in the model checking field, between compact representations versus strength and utility of counter-examples.” (Raad et al., 2020, p. 245)
“Abstraction techniques are typically used to increase compactness. This has the undesired side-effect that counterexamples become “abstract”: they may be infeasible, in that they may not actually witness a concrete execution that violates a given property” (Raad et al., 2020, p. 246)
“the under-approximating global bug hunters such as fuzzers [23] and symbolic executors [9], which suffer from scalability limitations but not false positives (at least, ideally)” (Raad et al., 2020, p. 246)
“compositional techniques can have less precision compared to global ones: examining all call sites of a procedure can naturally lead to more precise results.” (Raad et al., 2020, p. 246)