Peter W. O’Hearn, POPL20
类似于霍尔逻辑,但是为下近似。三元组的含义及对比详见 Non-termination Proving at Scale 中的 FUA。
从谓词变换的角度来看,以前置条件在语句作用下的最强后置条件为基准(不一定可计算)1,霍尔逻辑的后置条件为其上近似(更弱),IL 为下近似(更强)。
反过来,给定后置条件,满足 IL 三元组的前置条件不一定存在。要进行后向推理,文中的一种思路是先使用标准的后向谓词变换计算出前置条件,然后再前向计算(新的)后置条件。
In this paper we investigate the hypothesis that reasoning about the presence of bugs can be underpinned by sound techniques in a principled logical system, just as reasoning about correctness (absence of bugs) has been demonstrated to have sound logical principles in an extensive research literature.
Semantics of the Under-Approximate Triple
Definition
It means: the post-assertion result be an under-approximation (subset) of the final states that can be reached starting from states satisfying the presumption.
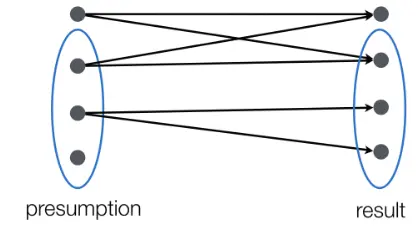
The triple is equivalent to backward reachability:

From the perspective of predicate transformer, result is stronger than (a subset of) the so-called strongest post-condition (a.k.a. strongest over-approximate post-condition):
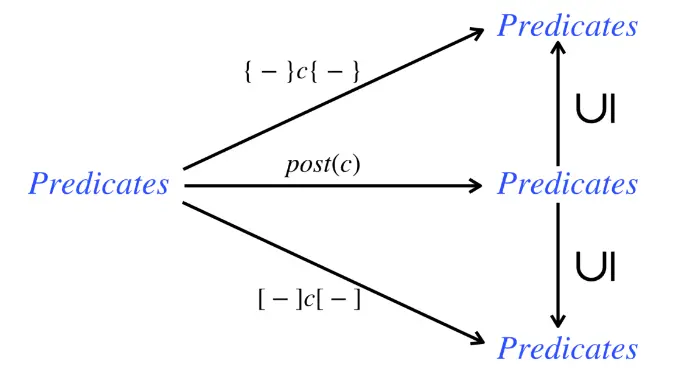
This condition is equivalently the weakest under-approximate post-condition.
The Proof System
Firstly, we add labels to post-condition to signify normal execution or errors.
The inference rules:


Note that, the Hoare-style (backwards-running) axiom for assignment is unsound for Incorrectness Logic. For example:
Properties
The proof system is sound and complete, in the same sense that Hoare Logic is sound and complete.
Predicate Transformer
Forward Transformer
Loops
For Hoare triple, the post() transformer can be written in terms of loop invariants:
Or equivalently defined by under-approximate triples:
which means we can under-approximate the post() predicate transformer by loop unrolling (bounded model checking).
It is a simple and surprisingly effective way to discover some post-conditions for a loop, but in general stronger reasoning is needed (as provided by the Backwards Variant rule).
Branches
The semantic definition is:
So instead of abandoning some path, we can define a under-approximate ‘join-operator’:
Backward Transformer
Given a relation r and assertion q, there need not exist any p such that [p]r [q]
Annotations
“In this paper we investigate the hypothesis that reasoning about the presence of bugs can be underpinned by sound techniques in a principled logical system, just as reasoning about correctness (absence of bugs) has been demonstrated to have sound logical principles in an extensive research literature.” (O’Hearn, 2020, p. 1) 🔤在本文中,我们探讨了这样一个假设:关于存在错误的推理可以建立在有原则的逻辑系统中的可靠技术之上,正如关于正确性(无错误)的推理已在广泛的研究文献中被证明具有可靠的逻辑原则一样。🔤
“Here we obtain a logic where instead one can prove the presence of bugs but not their absence” (O’Hearn, 2020, p. 2)
“how static reasoning about programs might be done, taking the perspective of bug catching instead of (only) proving absence of bugs” (O’Hearn, 2020, p. 2)
“It is important to note that the exact reasoning of the middle line of the diagram is definable mathematically but not computable (unless highly incomputable formulae are used to describe the post). Approximating in either direction provides a way to escape undecidability.” (O’Hearn, 2020, p. 4)
“But, the inability to prove an over-approximate spec (whether found by a tool or specified by a human) does not imply an error in a program, and neither does not having found a bug imply that there are none: thus, the need for dedicated techniques for each.” (O’Hearn, 2020, p. 5)
“People are sometimes led to an initial łyesž answer to the question above because they are unwittingly applying the rule of weakening the post-condition.” (O’Hearn, 2020, p. 5)
“What is more, soundly dropping disjuncts is a useful capability which can be called upon in order to help a reasoning tool scale.” (O’Hearn, 2020, p. 6)
“Even if we were mainly interested in incorrectness, under-approximate result assertions describing successful computations can help us soundly discover bugs that come after a procedure is called. In particular, if we were to have over-approximate assertions only for successful computations, then our reasoning could go wrong” (O’Hearn, 2020, p. 6)
“[p]C[ε: q]: q under-approximates the states when C exits via ε starting from states in p.” (O’Hearn, 2020, p. 7)
“Incorrectness logic uses Floyd’s forward-running assignment axiom (see Figure 3) rather than Hoare’s backwards-running one. We actually cannot use Hoare’s, which substitutes into the pre as [p[e/x]]x = e[ok: p], because it is unsound here;” (O’Hearn, 2020, p. 9)
“false is a valid result assertion for either normal or abnormal termination, for any program” (O’Hearn, 2020, p. 9)
“Conversely, we can drop conjuncts in the pre” (O’Hearn, 2020, p. 9)
“loop invariants don’t play a central role in under-approximate reasoning like they do for over-approximate” (O’Hearn, 2020, p. 9)
“The Unrolling Rule gives us a capability similar to symbolic bounded model checking [Clarke et al. 2004]. It is a simple and surprisingly effective way to discover some post-conditions for a loop, but in general stronger reasoning is needed (as provided by the Backwards Variant rule).” (O’Hearn, 2020, p. 9)
“This reachability property does not imply that a loop must terminate on all executions. Instead, it establishes that enough paths terminate to cover all the states in the result assertion, while allowing that other paths might lead to divergence” (O’Hearn, 2020, p. 10)
“We can cast the property as stated in terms of something happening by reading a spec backwards: for every state in the result, it is possible to eventually reach a state in the pre by executing backwards.” (O’Hearn, 2020, p. 10)