Proving Termination Through Conditional Termination

Borralleras, Cristina, Marc Brockschmidt, Daniel Larraz, Albert Oliveras, Enric Rodríguez-Carbonell, and Albert Rubio. ‘Proving Termination Through Conditional Termination’. In Tools and Algorithms for the Construction and Analysis of Systems, edited by Axel Legay and Tiziana Margaria, 99–117. Lecture Notes in Computer Science. Berlin, Heidelberg: Springer, 2017. https://doi.org/10.1007/978-3-662-54577-5_6.

termination proof via conditional termination

提出一种基于Max-SMT的conditional termination argument的综合方法。通过程序变形和safety checker，利用其组合出程序unconditional termination的证明

basic idea

• present a constraint-based method for proving conditional termination of integer program components.
• prove (unconditional) program termination using a mechanism to combine conditional termination proofs.

conditional termination

We say that a program P is (ℓ,φ)-conditionally terminating if every computation that contains a state (ℓ,v) with v⊨φ uses transitions from P only a finite number of times. In that case the assertion (ℓ,φ) is called a precondition for termination.

conditional inductive invariant

It’s the same as quasi-invariant in Proving Non-termination Using Max-SMT

synthesize conditional termination arguments

for a fixed 强连通分量 C of a program:

1. For all locations ℓ in C, we introduce templates $I_l$ corresponding to fixed-length conjunctions of linear inequalities on the program variables. These are templates of conditional inductive invariant
2. Furthermore, we also define a template R for a linear ranking function with integer coefficients
3. encode the constraints in a formula

the formula is

$$\mathbb{F}\stackrel{def}{=}\underset{\tau \in {\mathcal{E}}_{\mathcal{C}}}{\bigwedge }{\mathbb{I}}_{\tau }\wedge \underset{\tau \in \mathcal{I}}{\bigwedge }{\mathbb{C}}_{\tau }\wedge \underset{\tau \in \mathcal{M}}{\bigwedge }{\mathbb{N}}_{\tau }\wedge \underset{\tau \in \mathcal{M}}{\bigvee }({\mathbb{B}}_{\tau }\wedge {\mathbb{D}}_{\tau })$$

where the symbols are defined as follows ($\rho$ is the transition relation):

前两条是对invariant的约束，后三条是对ranking function R的约束。这里的定义和cvjapxqp中有些许差别，它只要求R在某一个转移上是递减且有下界的，在其它转移只要不增即可。

因此，这样的ranking function只保证一条转移终止（使用有限次）。要保证整个SCC是终止的，需要迭代地找这样的ranking function，直到每个边都被证明终止。见下。

${\bigwedge }_{\tau \in {\mathcal{E}}_{\mathcal{C}}}{\mathbb{I}}_{\tau }$是soft的（尽量保证unconditional termination），其余的约束是hard的（见Max-SMT）

unfolding and narrowing

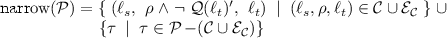
that is, any transition in a component is conjoined by the negation of the conditional invariant. The intuition is that, by the inductiveness of Q a computation that satisfies Q(ℓ) for a certain ℓ∈C cannot remain within C infinitely.

overall algorithm

Components are handled in sequence one at a time. For each component, preconditions for termination are computed. If, using a safety checker, we know that the condition always holds, then we have proved the unconditional termination.

Otherwise narrowing is applied and the process repeated.

If at some point the generation of preconditions for termination fails, then non-termination is attempted by calling an out-of-the-box non-termination prover

虽然这篇文章没有提出新的Nontermination Analysis方法，但是经过narrow之后的程序比原程序有更多的信息，所以在Termination Analysis失败后能利用其结果，提高证明非终止性的能力。