Concurrent Separation Logic

Peter O’Hearn, Resources, concurrency, and local reasoning & Stephan Brookes, A semantics for concurrent separation logic. TCS’07

分离逻辑原本用于对堆数据结构进行推理，设计了分离与等构造对这类数据结构的「共享」情况进行了限制。类似地，在并发程序中也存在资源的分离和共享，堆就是其中的一种资源。此时，分离逻辑公式不仅指示堆的值，也指示其所有权。例如，$e\mapsto e^{\prime }$ 可以解释为「e映射为e’，当前线程可以操作位置e，且其他线程一定不会操作e。」

“it was not long before O’Hearn made the critical observation that separation logic’s built-in support for interference resistance could be equally—if not even more—useful for reasoning about concurrent programs” (Jung 等, 2018, p. 3)

“they now denote ownership by whichever thread is running the code in question. Concretely, this means that if a thread t can assert l → v, then t knows that no other thread can read or write l concurrently, so it can completely ignore the other threads and just reason about as if it were operating in a sequential setting.” (Jung 等, 2018, p. 3)

如果线程各自操作分离的内存，则有下面的推导规则：

$\frac{\{P\}C\{Q\}\left\{P^{\prime }\right\}{C}^{\prime }\left\{Q^{\prime }\right\}}{\left\{P\ast P^{\prime }\right\}C\Vert C^{\prime }\left\{Q\ast Q^{\prime }\right\}}$

where C does not modify any variables free in P′, C′, Q′, and conversely.

与此对应的霍尔逻辑规则是Tony Hoare在‘Towards a Theory of Parallel Programming (1972)’提出的，不过霍尔逻辑是全局的，对数组的更新也是全局（a[i] = … 被认为改变了a），故实际应用不广泛。

所有权的动态转移

不过，线程间往往需要通过共享的资源进行通信。CSL支持所有权的动态转移（所有权并不属于程序语义，而是只用于证明的概念）。与之相对地则是基于语法静态确定临界区。下面的程序中信号量的使用确立了对地址10的互斥访问，但在语法上并没有清晰的临界区：

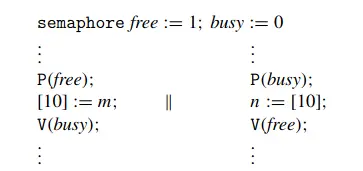
首先，CSL的一个基本假设是：

“Separation Property. At any time, the state can be partitioned into that owned by each process and each grouping of mutual exclusion.” (O’Hearn, 2007, p. 275)

“A crucial point is that the Separation Property does not presume a static, once and for all, partition of the state; it allows the partition to change over time.” (O’Hearn, 2007, p. 275)

如果程序状态在逻辑上无法被如此分离（比如有data race的情况 $x=x+1||x=x+1$），则CSL无效。

“Similarly, we do not check that the program satisfies the Separation Property at each step, and neither do we check that it satisfies the Ownership Hypothesis. Rather, the system is arranged to achieve these properties implicitly, for any program that gets past the proof rules.” (O’Hearn, 2007, p. 287)

“This mirrors a classic program design principle of Dijkstra, that ‘apart from the (rare) moments of explicit intercommunication, the individual processes are to be regarded as completely independent of each other’” (O’Hearn, 2007, p. 284)

如上所述，CSL中$e\mapsto e^{\prime }$表示线程当前对e的独占，而除了被某个线程占有外，e也可能被某项资源（比如信号量，条件临界区等）占有。这在本文中体现为资源不变式RI。资源不变式可以近似描述资源占有所有权的条件。当满足条件时，线程可以通过资源不变式获取所有权e，或者将所有权e放弃以保持资源不变式成立。

比如，在上述例子中，信号量s的资源不变式是

$R{I}_s=(s=0\wedge \text{emp})\vee (s=1\wedge 10\mapsto -).$

可以解读为「要么信号量s为0，且不具有任何所有权；要么信号量为1，具有地址10的所有权」

上述证明中：

• 信号量的P、V操作逻辑上获取和放弃了10的所有权，以此完成证明¹。
• 没有修改上面的Parallel规则，而是通过资源不变式规定同步原语的推导规则来实现
• 因此也不需要额外证明不相干性（如Owiki-Gries推理一般）
• 资源不变式属于额外的信息，可以认为在资源声明之后加入到证明的上下文中，即证明中操作的其实是相继式 $\Gamma ⊢\{P\}C\{Q\}$。这允许资源声明的嵌套

Brookes给出了CSL的语义以及可靠性证明，并说明了CSL能证明的程序一定是race-free的

Related

• Separation Logic

Footnotes

1. P的条件是s>0，对应不变式中有所有权的析取项；反之V对应没有所有权，并且在当前线程获得10的所有权时需要将其放弃（因为必须重建资源不变式，这由下面的同步原语推导规则规定） ↩
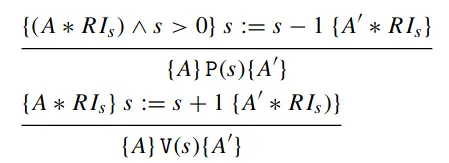